簡単な線形計画法問題の解法

f:id:fa11enprince:20120720075237j:plain
線形計画法、大学の講義かもしかしたら大学受験の時に
やっていたような気がするんですが、
毎度なんでか解き方忘れてしまって、
その場で時間をかけて考えてしまうんですよね。
いい加減、解法を丸暗記しないとなぁとメモです。
IT系の試験ではなぜか頻出です。

問題例

意図的に簡単な問題を出しています。
都合のいい問題を作り出すために
何度か書き換えているので間違いがあるかもしれません。

とある内職をしている美人な人妻A子が
部品Xと部品Yを作っています。
部品Xと部品Yの数により納品物ができ、
1つの納品物あたりのもらえるお金は
次の表に示すとおりです。
やる気の問題なのかよくA子にもわからないのですが、
部品Xの1日に作れる数は36個で、
部品Yの1日に作れる数は12個という謎の制約があります。
このとき、1日のもらえるお金を最大にするように部品Xと部品Yを作った時の
利益はいくらでしょうか。

	部品X	部品Y	お金(ドル)
納品物1	6	3	4
納品物2	1	2	3

解き方

中学校程度の数学知識があれば解けます。

制約条件を導きます

人妻A子の制約条件を式にすると以下です。
部品Xの数を $x$ として、部品Yの数を $y$ とします。
① $x \geqq 0$
② $y \geqq 0$
③ $6x + 3y \leqq 36$ (納品物1)
④ $1x + 2y \leqq 12$ (納品物2)
①、②は当たり前として、③、④は人妻の生産能力を表している式ですね。

目的関数を記述します

ここで、納品物1と納品物2を収めることによってもらえるお金を $z$ とします。
⑤ $z = 4x + 3y$

制約条件をグラフに書きます。

③、④を表したx, yの2次元グラフを書きます。
元の式のままでもx, yに具体的な数を入れてみて線を引っ張ってもよいのですが、
中学数学からのやり方になれている人がほとんどだと思いますので、
$y = ax + b$ の形に式変形をします。
③について
$3y \leqq -6x + 36$
$y \leqq -2x + 12$
傾き: -2, y軸の切片が12ですね。
④について
$2y \leqq -x + 12$
$y \leqq -\frac{1}{2}x + 6$
傾き: -1/2, y軸の切片が6ですね。
f:id:fa11enprince:20150714034449p:plain
こんな感じでしょうか(´・ω・`)

目的関数をざっくり書きます。

⑤について $z$ をとりあえず定数と見てやります
$3y = -4x + z$
$y = -\frac{4}{3}x + \frac{z}{3}$
このとき $z$ については全く重要でないので、-4/3の傾きのグラフを考えます。
そこで部品XとYで囲まれたの中で最大の値を取るところを探します。
本当にテキトーにひきます。
少なくとも部品XとYの間の傾きなのでそれさえわかってしまえばいいのです。
f:id:fa11enprince:20150714034848p:plain
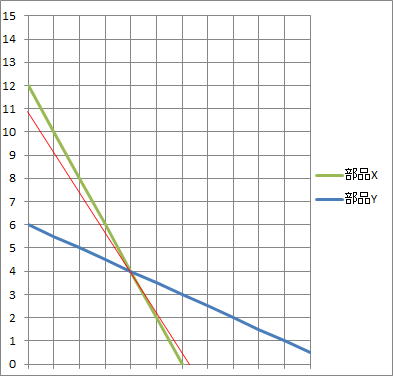
と、これを見ると交点の部分がちょうど最大だとわかるので、
③、④から方程式を解いてもよいのですが、(x, y) = (4, 4)だとわかります。
よって、最大のもらえるお金は
$z = 4 \times 4 + 3 \times 4$
で28となります。